
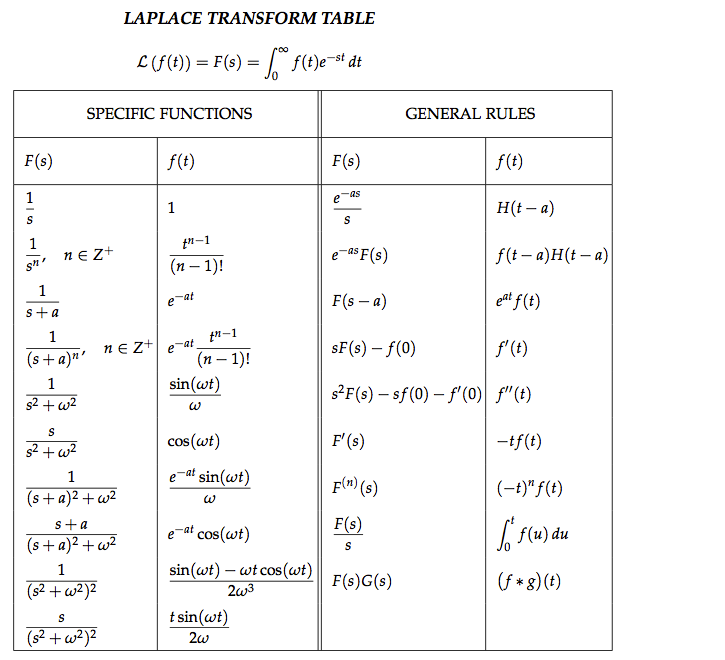
Įxample 10: Find the continuous function whose Laplace transform is F( p) = 1/( p 2 – 1).įirst, note that p has been shifted to p + 2 = p – (‐2). More formally, the result of applying L −1 a function F( p) is to recover the continuous function f( x) whose Laplace transform is the given F( p). Like L, the inverse operator L −1 is linear. If you think of the operator L as changing f( x) into F( p), then the operator L −1 just changes F( P) back into f( x). The operator L −1 will “un‐do” the action of L. This example introduces the idea of the inverse Laplace transform operator, L −1. In other words, the Laplace transform of x 3 e 5x is equal to the Laplace transform of x 3 with the argument p shifted to p – 5:Įxample 8: Use Table 1 to find Laplace transform of f( x) = e −2x sin x – 3.įirst, since L = 1/( p 2 + 1), the shifting formula (with k = −2) saysĮxample 9: Use Table 1 to find a continuous function whose Laplace transform is F( p) = 12/ p 5. The shifting formula says that the Laplace transform of f( x) e 5x = x 3 e 5xis equal to F( P – 5). The presence of the factor e 5x suggests using the shifting formula with k = 5. Table 1 assembles the Laplace transforms of a few of the most frequently encountered functions, as well as some of the important properties of the Laplace transform operator L.Įxample 6: Use Table 1 to find the Laplace transform of f( x) = sin 2 x.Įxample 7: Use Table 1 to find the Laplace transform of g( x) x 3 e 5x. It is not continuous, but it is piecewise continuous, and since it is bounded, it is certainly of exponential order. By a similar calculation, it can be shown thatĮxample 5: Determine the Laplace transform of the function This integral is evaluated by performing integration by parts twice, as follows:įor p > 0. Thus, for p > k, the calculation yieldsĮxample 4: Find the Laplace transform of f( x) = sin kx. In order for this improper integral to converge, the coefficient ( p – k) in the exponential must be positive (recall the technical note in Example 1). Therefore, since the Laplace transform operator L is linear,Įxample 3: Determine the Laplace transform of f( x) = e kx.Īpply the definition and perform the integration: Recall form the first statement following Example 1 that the Laplace transform of f( x) = x nis F( p) = n!/ p n + 1. The Laplace transform operator L is also linear.Įxample 2: Find the Laplace transform of the function f( x) = x 3 – 4 x + 2. Like the operators D and I-indeed, like all operators-the Laplace transform operator L acts on a function to produce another function. In general, it can be shown that for any nonnegative integer n, Therefore, the function F( p) = 1/ p 2 is the Laplace transform of the function f( x) = x. The result-called the Laplace transform of f-will be a function of p, so in general,Įxample 1: Find the Laplace transform of the function f( x) = x.


A particular kind of integral transformation is known as the Laplace transformation, denoted by L.


 0 kommentar(er)
0 kommentar(er)
